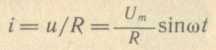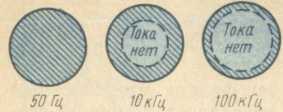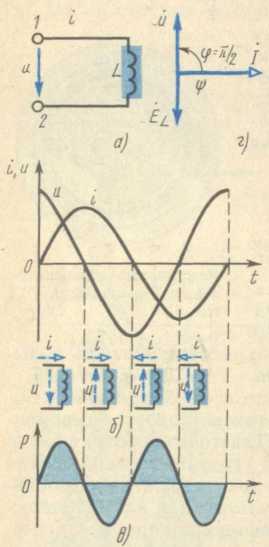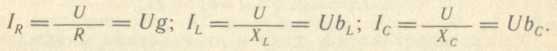§ 9. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ПЕРЕМЕННОГО ТОКА
Переменный ток имеет огромное практическое значение. Почти вся электроэнергия
вырабатывается в виде энергии переменного тока. Возможность получать переменный
ток различного напряжения — высокого для передачи энергии на большие расстояния,
низкого — для питания различных потребителей, простота устройства генераторов и
двигателей переменного тока, надежность их работы, удобство эксплуатации и
высокие технико-экономические показатели обеспечили переменному току
повсеместное широкое применение.
 |
|
Рис. 30. Временная диаграмма синусоидального
тока
|
В цепях переменного тока имеют дело с токами, эдс и
напряжениями, которые периодически изменяют направление и значение. Изменения
повторяются через некоторый промежуток T,
называемый периодом.
Число периодов в секунду называется
частотой
f.
Широко используется и очень удобен для изучения синусоидальный ток.
На рис. 30 приведено графическое изображение (временная диаграмма)
синусоидального тока. Его мгновенное значение описывается формулой

где
Im
— максимальное значение (амплитуда) тока;
 =2
=2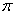 /Т=2
/Т=2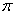 f
— угловая частота;
f
— угловая частота;
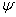 —
начальная фаза (значение аргумента в начальный момент времени, т. е. при t
= 0).
—
начальная фаза (значение аргумента в начальный момент времени, т. е. при t
= 0).
Период выражают в секундах [с], частоту — в герцах [Гц], фазу — в радианах [рад]
или градусах [град], угловую частоту — в радианах на секунду [рад/с].
► Все сказанное о синусоидальном токе относится также
к синусоидальным эдс и напряжению.
 |
|
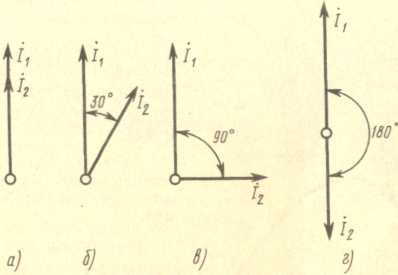
Рис. 31. Векторные диаграммы для токов с
различным сдвигом фаз
|
Действующее значение. Энергетическое действие тока (тепловое и
способность совершать механическую работу) характеризуется его
действующим значением.
Между действующими и амплитудными значениями синусоидальных величин существуют
соотношения:
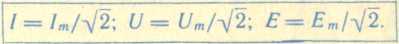
► На шкалы амперметров и вольтметров переменного тока
обычно наносят действующие значения тока и напряжения.
Векторные диаграммы. При рассмотрении многих вопросов, связанных с цепями
синусоидального тока, в частности при их расчетах, удобно пользоваться
векторными диаграммами. Они позволяют изображать синусоидальные величины
проще, нежели с помощью временных диаграмм.
 |
|
 |
|
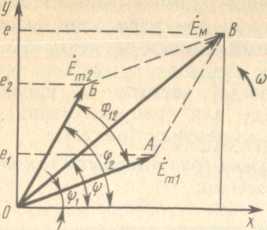
Рис. 32. Сложение двух векторов эдс
|
|
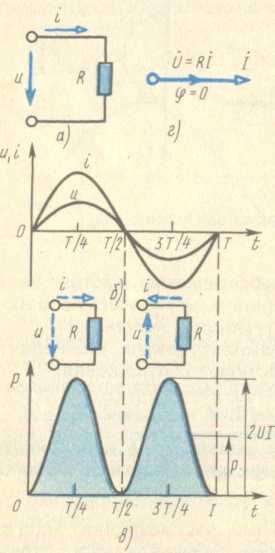
Рис. 33. Схема (а) электрической цепи с
активным сопротивлением, графики мгновенных значений напряжения,
тока (б) и мощности (в), а также векторная
диаграмма (г)
|
Метод векторных диаграмм
состоит в следующем. Переменные токи, напряжения, эдс изображают в виде
векторов, которые обозначают соответствующей прописной буквой с точкой:
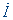 ,
,
 ,
,
 .
Векторы изображают неподвижными, с учетом сдвига по фазе и подразумевают, что
они равномерно вращаются против часовой стрелки с угловой скоростью
.
Векторы изображают неподвижными, с учетом сдвига по фазе и подразумевают, что
они равномерно вращаются против часовой стрелки с угловой скоростью
 .
При таком вращении вектора его проекция на вертикальную ось изменяется во
времени по закону синуса с учетом начальной фазы.
.
При таком вращении вектора его проекция на вертикальную ось изменяется во
времени по закону синуса с учетом начальной фазы.
На рис. 31, а—г для примера показаны векторные диаграммы двух
токов, сдвинутых на 0, 30, 90 и 180°.
Сложение синусоидальных величин можно заменить
сложением векторов, их изображающих.
Например, на рис. 32 приведено сложение двух синусоидальных эдс:
е1=Еm1·sin( t+
t+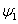 )
и е2=Еm2·sin(
)
и е2=Еm2·sin( t+
t+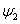 ),
представленных векторами
),
представленных векторами
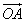 и
и
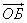 .
.
Результат сложения — вектор
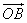 ,
которому соответствует е=Еm·sin(
,
которому соответствует е=Еm·sin( t+
t+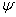 ).
Обычно на векторных диаграммах изображают действующие значения
токов, напряжений, эдс.
).
Обычно на векторных диаграммах изображают действующие значения
токов, напряжений, эдс.
Простейшие цепи переменного тока. Самой простейшей цепью является цепь с
одним сопротивлением R (рис. 33, а). При синусоидальном напряжении на
зажимах u=Um·sin t
ток в цепи с сопротивлением R по закону Ома
t
ток в цепи с сопротивлением R по закону Ома
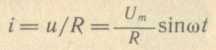
синусоидальный и совпадает по фазе с приложенным напряжением.
На рис. 33 это показано с помощью временной (б) и векторной (г)
диаграмм. Амплитуде тока Im=Um/R
соответствует и действующее значение I=U/R.
Сопротивление R называется активным сопротивлением цепи.
Проводимость цепи g=1/R.
 |
|
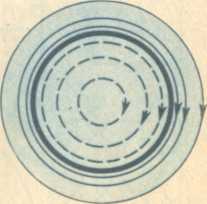
Рис. 34. Магнитное поле вокруг проводника с
током
|
Мгновенные значения мощности определяются произведением мгновенных значений тока
и напряжения. Как показано на построенном таким образом рис. 33, в,
мощность всегда положительна. Средняя потребляемая в цепи мощность

называется
активной мощностью и выражается в ваттах [Вт].
Поверхностный эффект. Активное сопротивление для проводников всегда
больше омического сопротивления постоянному току вследствие так называемого
поверхностного эффекта.
Поверхностный эффект обусловлен следующим. Вокруг проводника с переменным током
создается переменное магнитное поле (рис. 34). Для токов, проходящих в
центральной части проводника, создается наибольшая эдс самоиндукции, так как эти
токи окружены наибольшим магнитным потоком. В результате ток как бы вытесняется
во внешнюю часть проводника, «рабочее сечение» проводника уменьшается и
сопротивление возрастает. На частоте 50 Гц этот эффект почти отсутствует, но он
очень сильно проявляется на высоких частотах (рис. 35).
Цепь с индуктивной катушкой. Рассмотрим цепь с идеальной (не обладающей
активным сопротивлением) катушкой индуктивности (рис. 36, а).
При прохождении синусоидального тока i=Im·sin t
напряжение на катушке uL=L(∆i/∆t).
Оно синусоидальное и в момент наибольшей скорости изменения тока
∆i/∆t
(при переходе через нулевое значение) достигает наибольшего значения. При
нулевой скорости изменения тока (при переходе через амплитудное значение)
напряжение на катушке равно нулю (рис. 36, б).
t
напряжение на катушке uL=L(∆i/∆t).
Оно синусоидальное и в момент наибольшей скорости изменения тока
∆i/∆t
(при переходе через нулевое значение) достигает наибольшего значения. При
нулевой скорости изменения тока (при переходе через амплитудное значение)
напряжение на катушке равно нулю (рис. 36, б).
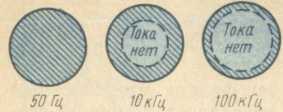 |
|
Рис. 35. Явление поверхностного эффекта при
различной частоте тока (рабочее сечение провода заштриховано)
|
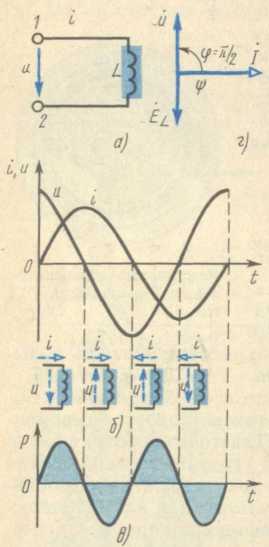 |
|
Рис. 36. Схема (а) электрической цепи с
индуктивной катушкой, графики мгновенных значений тока,
напряжения (б) и мощности (в), а также векторная
диаграмма (г)
|
Таким образом, в идеальной катушке индуктивности угол
сдвига фаз между напряжением и током равен
 /2
(90°), причем напряжение по фазе опережает ток, как показано на векторной
диаграмме (рис. 36, г).
/2
(90°), причем напряжение по фазе опережает ток, как показано на векторной
диаграмме (рис. 36, г).
Через некоторый очень малый промежуток времени
∆t
после того, как i был равен нулю,
∆i=Im·sin ∆t≈Im
∆t≈Im ∆t,
поскольку для малых аргументов sin
∆t,
поскольку для малых аргументов sin ∆t≈
∆t≈ ∆t.
Тогда uL=Um=L(Im
∆t.
Тогда uL=Um=L(Im ∆t
/∆t)=L·Im
∆t
/∆t)=L·Im .
.
Величину Um/Im=U/I= L=XL
называют индуктивным сопротивлением.
Она определяет способность индуктивной катушки противодействовать прохождению
переменного тока и выражается в омах.
L=XL
называют индуктивным сопротивлением.
Она определяет способность индуктивной катушки противодействовать прохождению
переменного тока и выражается в омах.
Чем больше
 и
L, тем выше XL. Проводимость цепи bL=
1/ХL.
и
L, тем выше XL. Проводимость цепи bL=
1/ХL.
Мгновенное значение мощности в рассматриваемой цепи может быть найдено как
произведение мгновенных значений тока и напряжения и, как видно из рис. 36, в,
изменяется по синусоидальному закону с частотой 2 .
.
Очевидно, что активная мощность цепи равна нулю.
► При положительном значении мощности она
потребляется индуктивностью, при отрицательном отдается обратно источнику. Такое
энергетическое состояние цепи характеризуется так называемой реактивной
мощностью QL=I2 L=ULI.
Единица реактивной мощности вольт-ампер реактивный (вар).
L=ULI.
Единица реактивной мощности вольт-ампер реактивный (вар).
 |
|
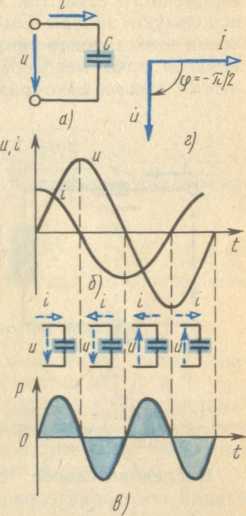
Рис. 37. Схема (а) электрической цепи с
конденсатором, графики мгновенных значений тока, напряжения (б)
и мощности (в), а также векторная диаграмма (г)
|
Цепь с конденсатором. Рассмотрим цепь (рис. 37, а) с
конденсатором, к зажимам которой приложено напряжение u=Um·sin t
t
Ток в цепи конденсатора iC=C(∆u/∆t).
В момент наибольшей скорости изменения напряжения (при переходе через нулевое
значение) через конденсатор протекает максимальный ток. Если напряжение не
меняется во времени (при переходе через амплитудное значение), ток конденсатора
равен нулю (рис. 37, б).
Таким образом, в конденсаторе угол сдвига между
напряжением и током также равен
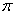 /2
(90°), причем по фазе напряжение отстает от тока, как показано на векторной
диаграмме (рис. 37, г).
/2
(90°), причем по фазе напряжение отстает от тока, как показано на векторной
диаграмме (рис. 37, г).
В момент времени ∆t
после прохождения кривой синусоидального напряжения через нуль можно записать:
∆u=Um·sin ∆t≈Um
∆t≈Um ∆t.
Тогда i=Im=C(Um
∆t.
Тогда i=Im=C(Um ∆t
/∆t)=C·Um
∆t
/∆t)=C·Um .
.
Величина Um/Im=U/I=1/( C)=XC
называется емкостным сопротивлением. Оно определяет способность конденсатора
уменьшать переменный ток и выражается в омах.
C)=XC
называется емкостным сопротивлением. Оно определяет способность конденсатора
уменьшать переменный ток и выражается в омах.
Чем больше С и
 ,
тем меньше емкостное сопротивление. Проводимость цепи bC=
1/ХC.
,
тем меньше емкостное сопротивление. Проводимость цепи bC=
1/ХC.
Энергетическое состояние цепи характеризуется обменом энергии между
конденсатором и источником (рис. 37, в). Этому процессу соответствует
реактивная мощность.
Индуктивное и емкостное сопротивления называют
реактивными. В связи с различием фазовых
сдвигов тока и напряжения на индук тивности и емкости условно принято считать
индуктивное сопротив ление потребителем, а емкостное — генератором реактивной
мощности.
Расчет цепей переменного тока. При расчетах цепей переменного тока, так
же как и цепей постоянного тока, используют законы Ома и Кирхгофа. Отличие в
применении этих законов заключается в том, что в цепях переменного тока
необходимо учитывать углы сдвига фаз между токами и напряжениями.
 |
|
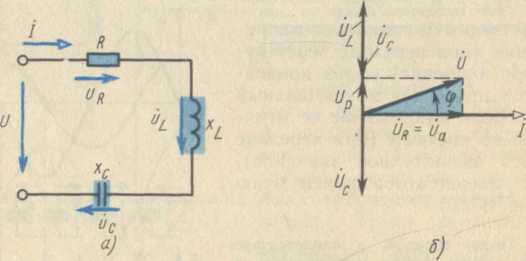
Рис. 38. Схема (а) цепи с
последовательным соединением R,
L и С элементов и ее векторная диаграмма (б)
|
Последовательное соединение. Рассмотрим общий случай последовательного
соединения резистора, катушки индуктивности и конденсатора (рис. 38, а).
Для падений напряжения на отдельных элементах можно записать: UR=I·R,
UL=I·ХL,
UС=I·ХС.
Эти падения напряжения имеют соответствующие углы сдвига фаз по отношению к
общему току цепи I.
На векторной диаграмме (рис. 38, б) отложены векторы
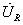 ,
,
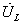 ,
,
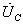 и
сложением их построен вектор
и
сложением их построен вектор
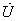 ,
имеющий активную
,
имеющий активную
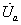 =
=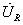 и реактивную
и реактивную
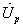 =
=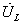 +
+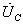 составляющие. Для суммарного напряжения U
можно записать:
составляющие. Для суммарного напряжения U
можно записать:
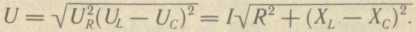
Величина
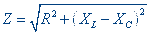 называется
полным сопротивлением цепи
и выражается в омах.
называется
полным сопротивлением цепи
и выражается в омах.
► Соотношение U/I=Z
— выражение закона Ома для цепи переменного тока. Полная проводимость цепи
y=1/Z.
Угол сдвига фаз между током и напряжением цепи определяется
тригонометрическими функциями соs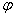 =UR/U=R/Z;
sin
=UR/U=R/Z;
sin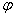 =(UL—UC)/U=(ХL—ХC)/Z.
Если ХL >
ХC, то вектор
=(UL—UC)/U=(ХL—ХC)/Z.
Если ХL >
ХC, то вектор
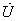 опережает
вектор
опережает
вектор
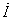 ,
если ХL < ХC, то
,
если ХL < ХC, то
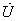 отстает
от
отстает
от
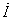 .
.
Активная мощность цепи

реактивная мощность
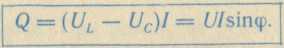
Произведение действующих значений напряжения и тока
цепи называется полной мощностью цепи:
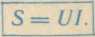
Очевидно, что
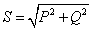 ,
так как sin2
,
так как sin2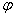 +соs2
+соs2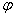 =1.
=1.
Величина соs называется коэффициентом мощности.
называется коэффициентом мощности.
Резонанс напряжений. В рассмотренной цепи с последовательным соединением
элементов R, L
и С при равенстве реактивных сопротивлений XL
и XC
имеет место так называемый резонанс напряжений. Так как эти сопротивления
зависят от частоты, резонанс наступает при некоторой
резонансной частоте
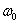 :
:
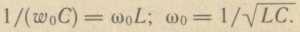
Общее сопротивление цепи в этом случае минимальное и чисто активное
Z=R, а ток имеет максимальное значение. При
 <
<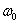 нагрузка имеет активно-емкостный характер, при
нагрузка имеет активно-емкостный характер, при
 >
>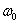 — активно-индуктивный.
— активно-индуктивный.
► При заданной частоте
 резонанс
может быть достигнут изменением L
или С.
резонанс
может быть достигнут изменением L
или С.
Следует отметить, что резкому увеличению тока в цепи при резонансе соответствует
возрастание UL
и UC. Эти напряжения могут стать значительно больше
напряжения 0, приложенного к зажимам цепи, поэтому резонанс напряжений —
явление, опасное для электроэнергетических установок.
В технике связи и в автоматике явление резонанса напряжений широко используют
для настройки приемных и передающих устройств на определенную частоту.
Параллельное соединение. Токи в ветвях параллельно соединенных элементов
цепей имеют соответствующий фазовый сдвиг по отношению к общему напряжению этих
цепей. Поэтому общий ток цепи равен сумме токов отдельных ее ветвей с учетом
фазовых сдвигов. Иначе говоря, в этом случае вектор общего тока определяется
суммой векторов токов параллельных ветвей.
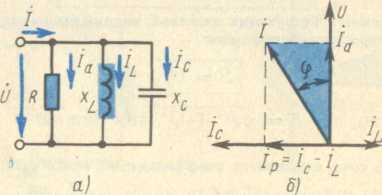
Рассмотрим параллельное соединение трех элементов, обладающих активным
сопротивлением R, индуктивным XL
и емкостным XC
(рис. 39, а).
 |
|
Рис. 39. Схема (а) параллельной цепи с
активным, индуктивным и емкостным сопротивлениями и векторная
диаграмма (б) для ее расчета
|
Для токов ветвей можно записать:
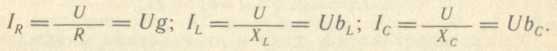
На векторной диаграмме (рис. 39, б) отложены векторы
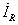 ,
,
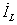 ,
,
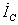 и
сложением их построен вектор
и
сложением их построен вектор
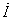 ,
имеющий активную
,
имеющий активную
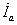 =
=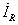 и реактивную
и реактивную
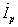 =
=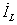 +
+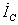 составляющие. Для суммарного тока I
имеем:
составляющие. Для суммарного тока I
имеем:
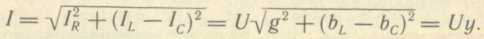
Угол сдвига фаз
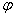 между
током I и напряжением U
определяется тригонометрическими функциями: соs
между
током I и напряжением U
определяется тригонометрическими функциями: соs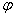 =IR/I=g/y;
sin
=IR/I=g/y;
sin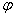 =(IL—IC)/I=(bL—bC)/y.
=(IL—IC)/I=(bL—bC)/y.
Если bL>bC, то нагрузка в
целом носит активно-индуктивный характер (вектор
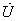 опережает
опережает
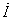 ),
если bL<bC
— активно-емкостный (вектор
),
если bL<bC
— активно-емкостный (вектор
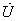 отстает
от вектора
отстает
от вектора
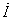 на
угол
на
угол
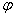 ).
).
Активная мощность цепи

реактивная мощность
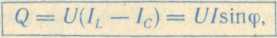
полная мощность

Резонанс токов. При равенстве реактивных сопротивлений ХC=ХL,
в цепи с параллельным соединением элементов R,
L, С возникает резонанс токов. Ток при резонансе достигает
минимального значения I=U/R, а соs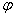 — максимального (соs
— максимального (соs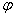 =1).
=1).
Значение резонансной частоты определяется формулой:
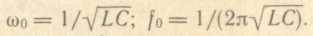
► Токи в ветвях, содержащих
L
и С, при резонансе могут быть больше общего тока цепи.
Индуктивный и емкостной токи противоположны по фазе,
равны по значению и по отношению к источнику энергии взаимно компенсируются, т.
е. идет обмен энергией между индуктивной катушкой и конденсатором.
Реактивная мощность цепи при резонансе токов равна нулю, поскольку равны и
противоположно направлены токи IL
и IC. Иными словами, реактивная мощность, потребляемая
в XL, равна реактивной мощности, генерируемой в XC.
Компенсация реактивной мощности. Режим, близкий к резонансу токов, широко
используют для повышения коэффициента мощности соs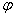 потребителей электроэнергии. Ток большинства потребителей электроэнергии носит
активно-индуктивный характер, т. е. имеет активную и индуктивную составляющие.
Включая параллельно потребителям батареи конденсаторов, разгружают источники
энергии и линию от реактивного тока. Индуктивный ток потребителей компенсируется
емкостным током конденсаторов. В результате с помощью компенсации достигают
значений соs
потребителей электроэнергии. Ток большинства потребителей электроэнергии носит
активно-индуктивный характер, т. е. имеет активную и индуктивную составляющие.
Включая параллельно потребителям батареи конденсаторов, разгружают источники
энергии и линию от реактивного тока. Индуктивный ток потребителей компенсируется
емкостным током конденсаторов. В результате с помощью компенсации достигают
значений соs =0,85÷0,95.
Это дает значительный экономический эффект из-за разгрузки проводов, снижения
потерь, экономии материалов и электроэнергии.
=0,85÷0,95.
Это дает значительный экономический эффект из-за разгрузки проводов, снижения
потерь, экономии материалов и электроэнергии.