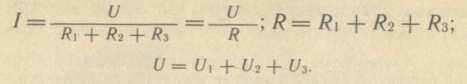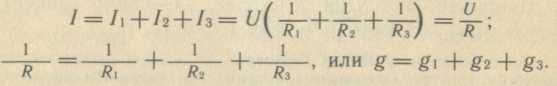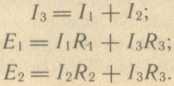§ 6. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ПОСТОЯННОГО ТОКА
► В цепях постоянного тока имеют дело с
электродвижущими силами (эдс), токами и напряжениями, которые не изменяются с
течением времени.
В этих цепях источниками электроэнергии могут быть выпрямители, генераторы
постоянного тока, аккумуляторы и гальванические элементы. В них происходит
преобразование других видов энергии в электрическую энергию постоянного тока.
В приемниках (электродвигателях, нагревателях, электролитических ваннах, лампах
накаливания и других устройствах) электрическая энергия постоянного тока
преобразуется в механическую, тепловую, химическую, световую и другие виды
энергии.
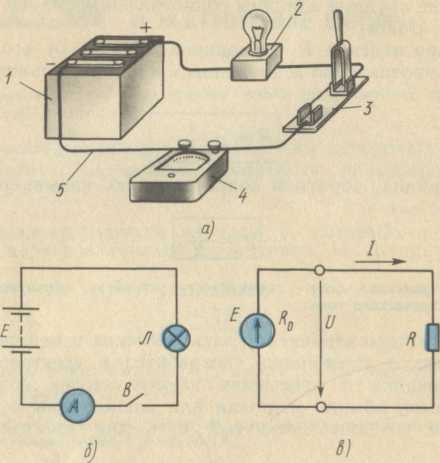
В качестве примера на рис. 13, а приведена простейшая электрическая цепь,
состоящая из батареи аккумуляторов 1, лампы накаливания 2,
выключателя 3, амперметра 4
и соединительных проводов 5. Такой цепи соответствуют электрическая и
расчетная схемы, представленные на рис. 13, б, в соответственно.
 |
|
Рис. 13. Простейшая электрическая цепь
постоянного тока (а) и ее принципиальная (б), а
также расчетная (в) схемы
|
Закон Ома. Закон Ома устанавливает зависимость между напряжением и током.
В применении к участку цепи (не содержащему источника
тока) он формулируется следующим образом: ток на участке электрической цепи
равен напряжению на зажимах этого участка, деленному на его сопротивление:

Соотношение между эдс, сопротивлением и током в замкнутой цепи согласно закону
Ома выражается формулой
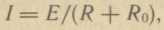
где
R — сопротивление внешней части цепи; R0 — внутреннее
сопротивление источника.
Сложные электрические цепи. Сложные электрические цепи характеризуются
наличием ветвей, узлов, контуров.
Ветвь
— участок цепи, вдоль которого проходит один и тот же ток и который состоит из
последовательно соединенных элементов.
Узел
— место соединения трех ветвей и более.
Контур
— любой замкнутый путь цепи, который можно обойти, двигаясь по ее ветвям.
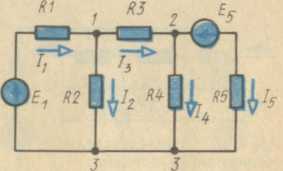
Например, цепь на рис. 14 состоит из пяти ветвей, трех узлов, шести контуров.
Расчеты электрических цепей производят с помощью законов Кирхгофа. При этом в
большинстве случаев приемники электроэнергии, включенные в цепь постоянного
тока, можно рассматривать как резисторы, имеющие те же сопротивления, что и
реальные приемники. В схемах резисторы обозначаются R1,
R2, R3, ..., их сопротивления в расчетах R1,
R2, R3....
Согласно первому
закону Кирхгофа сумма токов,
направленных к узлу электрической цепи, равна сумме токов, направленных от него.
Причем направления токов к узлу считаются положительными, от узла —
отрицательными.
Например, для узла 2 на рис. 14 можно записать: I3
= I4 + I5; Для узла 3:
I2
+ I4 + I5=I1.
Согласно второму
закону Кирхгофа во всяком замкнутом
электрическом контуре алгебраическая сумма эдс равна алгебраической сумме
напряжений на сопротивлениях, входящих в этот контур. При этом значения эдс и
напряжений считают положительными, если направления эдс и токов совпадают с
выбранным направлением обхода контура.
Например, для внешнего контура схемы на рис. 14 можно записать:
E1-E5=
I1R1+I2R2+I3R3;
для внутреннего контура: 0=I3R3+I4R4-I2R2.
 |
|
Рис. 14. Сложная электрическая цепь
|
Соединение приемников электроэнергии. В электрических схемах часто имеют
дело с последовательным, параллельным, смешанным соединением резисторов. Ток
I и суммарное эквивалентное сопротивление R
при различных способах соединения резисторов определяются следующим образом:
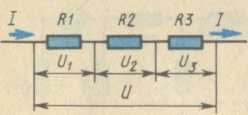
последовательное соединение (рис. 15)
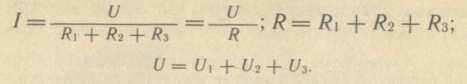
 |
|
Рис. 15. Последовательное соединение резисторов
|
 |
|
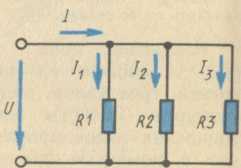
Рис. 16. Параллельное соединение резисторов
|
 |
|
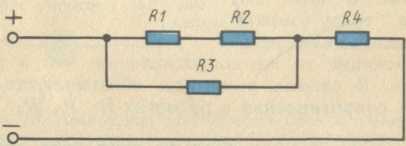
Рис. 17. Смешанное соединение резисторов
|
параллельное соединение (рис. 16)
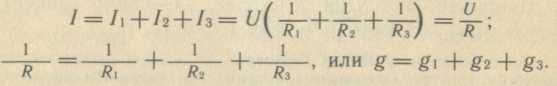
В частном случае параллельного соединения двух резисторов R1
и R2:
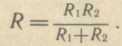
При смешанном соединении определение эквивалентного сопротивления цепи
производится поэтапно. Например, в схеме на рис. 17 сначала определяется
сопротивление R12
последовательно включенных резисторов R1
и R2
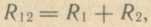
затем эквивалентное сопротивление параллельно соединенных резисторов с
сопротивлениями R12 и
R3.
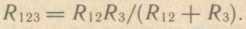
Наконец, находят общее сопротивление всей цепи:
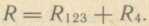
Аналогично поступают и при расчете более сложных схем со смешанным соединением
резисторов.
 |
|
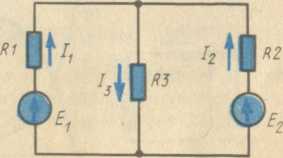
Рис. 18. К расчету сложных электрических цепей
|
Расчет сложных электрических цепей. Сложные электрические цепи с
несколькими контурами и различным размещением в них источников и потребителей
энергии в общем случае нельзя свести к сочетанию параллельно и последовательно
соединенных резисторов.
Для расчета сложных цепей используют различные методы. Наиболее общим является
метод составления и решения уравнений по законам Кирхгофа.
► Перед составлением уравнений произвольно задают
направление токов в ветвях, показав их на схеме стрелками.
Число необходимых уравнений равно числу неизвестных
токов, причем число уравнений по первому закону Кирхгофа должно быть на одно
меньше числа узлов цепи. Остальные уравнения составляют по второму закону
Кирхгофа, причем следует выбирать контуры наиболее простые и такие, чтобы в
каждом из них имелась хотя бы одна ветвь, не входящая в ранее составленные
уравнения.
Рассмотрим для примера схему, показанную на рис. 18. Для нее может быть
составлена система уравнений:
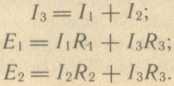
Решая эту систему уравнений, можно, например, определить токи I1,
I2, I3, если известны Е1,
Е2, R1
R2, R3.
Электрическая энергия и мощность. Для переноса заряда q
по участку цепи с напряжением U на его концах расходуется энергия:

Мощность
— это расход энергии в единицу времени:

 |
|
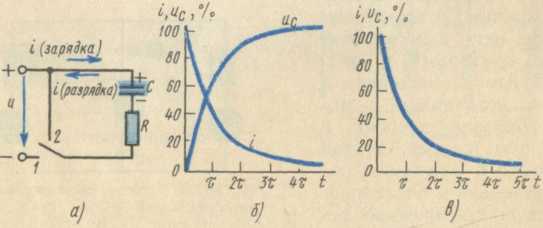
Рис. 19. Схема (а) для описания
процессов зарядки и разрядки конденсатора, а также изменение
тока и напряжения при его зарядке (б) и разрядке (в)
|
Учитывая закон Ома, можно получить другие выражения для мощности электрического
тока на участке цепи с сопротивлением R:
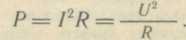
При использовании основных единиц (кулон, ампер, вольт, ом, секунда) мощность
выражается в ваттах, энергия — в джоулях.
Конденсатор в цепи постоянного тока. Большое практическое значение в
электротехнике имеет процесс зарядки и разрядки конденсатора.
При замыкании цепи, схема которой представлена на рис. 19, а, конденсатор
емкостью С заряжается. При этом ток зарядки и напряжение на конденсаторе
(рис. 19, б) изменяются согласно выражениям:
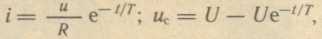
где
i, uс
— мгновенные значения тока и напряжения, е — основание натуральных
логарифмов.
При замыкании заряженного конденсатора на резистор R
ток разрядки и напряжение на конденсаторе изменяются по закону (рис. 19, в):
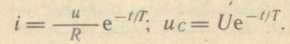
Скорость протекания процессов характеризуется постоянной времени
Т=RС, выражаемой в секундах.